Исходники Atrium
https://github.com/gecko0307/atrium
В ближайшем будущем также будет обновлена страница проекта.
Новая демка Atrium
Скачиваем новую демку с тенями:
Для Windows (2,36 МБ)
Для Linux (3,89 МБ)
Под Windows запускайте с параметром --enableShadows=1, либо используйте прилагающийся bat-файл, в котором этот параметр уже указан.
Репозиторий Atrium на GitHub также будет обновлен в ближайшее время.
Spider-Man: The Ultimate Fighter
 В раздел «Игры» добавлен еще один раритет: моя игра 2006 года «Spider-Man: The Ultimate Fighter», 2D-файтинг с Человеком-пауком в главной роли. Есть три уровня с возрастающей сложностью — вы должны победить зомби, Скорпиона и Росомаху. Относительно мощный (для игры на Game Maker) искусственный интеллект: с некоторыми врагами одержать победу с первого раза будет непросто.Управление: стрелки влево/вправо — перемещение, стрелка вверх — прыжок, пробел — удар, пробел + влево/вправо — выстрел паутиной, Escape — пауза, F6 — пропустить уровень. Есть также поддержка джойстика (вместо пробела — кнопка 1).
В раздел «Игры» добавлен еще один раритет: моя игра 2006 года «Spider-Man: The Ultimate Fighter», 2D-файтинг с Человеком-пауком в главной роли. Есть три уровня с возрастающей сложностью — вы должны победить зомби, Скорпиона и Росомаху. Относительно мощный (для игры на Game Maker) искусственный интеллект: с некоторыми врагами одержать победу с первого раза будет непросто.Управление: стрелки влево/вправо — перемещение, стрелка вверх — прыжок, пробел — удар, пробел + влево/вправо — выстрел паутиной, Escape — пауза, F6 — пропустить уровень. Есть также поддержка джойстика (вместо пробела — кнопка 1).
В архив, как обычно, включены все исходные материалы (под Public Domain).
7 лет с Linux
Именно такой у меня «стаж». С некоторых пор я вовсе перестал активно пользоваться Windows — под Linux у меня буквально все: работа, учеба, хобби и развлечения. Начиналась вся эта история достаточно забавно: я сам очень люблю читать подобные статьи-воспоминания, поэтому хочу поделиться и своими.
Мое знакомство с Linux началось в 2006-2007 годах благодаря нижегородскому журналу «Мой друг компьютер». Помимо информации для начинающих пользователей ПК, различных обзоров софта и железа, он содержал и материалы по Linux — рецензии на дистрибутивы, инструкции по установке, полезные команды Bash, различные советы и хитрости по эксплуатации linux-систем.
Я мгновенно влюбился — пусть и «дистанционно». Забавно вспомнить: в то время у меня еще не было безлимитного подключения к Интернету, и скачать даже самый маленький дистрибутив было проблематично (с помегабайтной тарификацией и 10 Мб казались заоблачной цифрой). В компьютерных магазинах диски с этой системой тогда тоже почему-то было не найти, поэтому попробовать Linux на практике мне долгое время не удавалось — и я помногу перечитывал подшивку «МДК», смаковал, запоминал информацию…
В одном из номеров был опубликован обзор Ubuntu — тогда еще молодой и малоизвестной системы на основе Debian. Позиционировалась она как дружелюбный дистрибутив для начинающих, и отдельно подчеркивалась возможность запуска системы прямо с CD, без необходимости установки. Особенно поразила меня щедрость разработчиков: компания Canonical тогда бесплатно рассылала диски с Ubuntu по почте — для тех, кто не имеет возможности скачать ее. Ведь это же как раз про меня!
Я тут же оформил заказ, и через пару месяцев в руках у меня был диковинный заграничный пакет, а внутри — симпатично оформленный LiveCD с Ubuntu 7.10. Моему восторгу не было предела! Впрочем, радоваться, как выяснилось, было особо нечему: LiveCD запустился, но, то ли из-за бага в видеодрайверах, то ли из-за неправильных настроек, изображение на экране было ужасным: сквозь дико смещенные и постоянно подрагивающие ряды пикселей с трудом узнавался рабочий стол GNOME. Нечего было и думать о том, чтобы устанавливать систему в таком состоянии на жесткий диск…
Уже впоследствии я узнал, какой бардак творится с видео в Linux: о глючности драйверов ATI ходили легенды и анекдоты. У меня же был старый ноутбук с интегрированной видеокартой Intel, и поиск стабильно работающего на нем дистрибутива отнял в свое время не одну неделю.
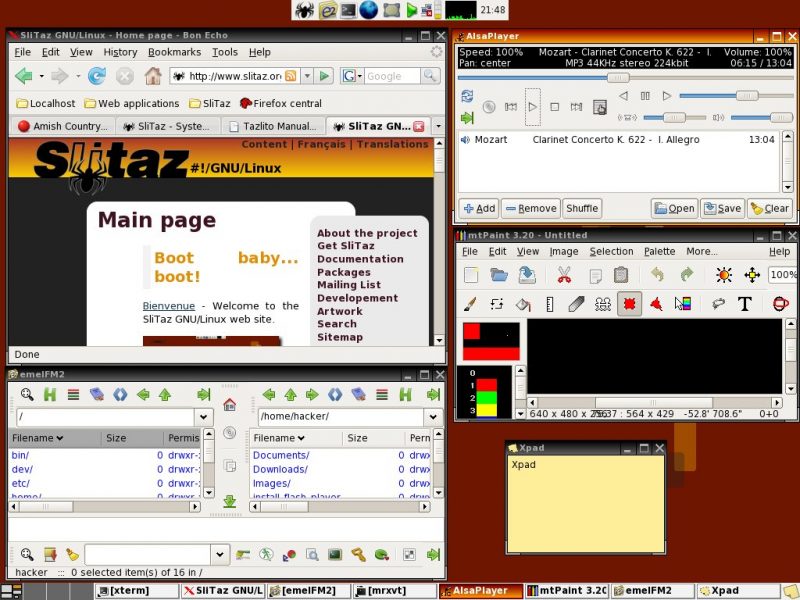 Осенью 2008 года у меня, наконец-то, появилась безлимитка по телевизионному кабелю. Правда, на ужасающе низкой скорости — почти на уровне dial-up, менее 64 кб/c. Но и этого хватало, чтобы кое-как выкачать Slitaz — мой первый полноценно работающий дистрибутив. Узнал я о нем на сайте http://distrowatch.com — тогда это был самый авторитетный ресурс по Linux, на него неизменно ссылались все авторы статей «МДК».
Осенью 2008 года у меня, наконец-то, появилась безлимитка по телевизионному кабелю. Правда, на ужасающе низкой скорости — почти на уровне dial-up, менее 64 кб/c. Но и этого хватало, чтобы кое-как выкачать Slitaz — мой первый полноценно работающий дистрибутив. Узнал я о нем на сайте http://distrowatch.com — тогда это был самый авторитетный ресурс по Linux, на него неизменно ссылались все авторы статей «МДК».
При весе в 30 мегабайт Slitaz включал полноценный графический режим (Xvesa вместо Xorg, рабочий стол Openbox) и достаточно богатый для такого размера набор пркладных программ (аудиоплеер, браузер, текстовый редактор, просмотровщик изображений, простенький графический редактор наподобие Paint и даже несколько игр). Правда, в той версии дистрибутива не работала сеть, поэтому приходилось постоянно переключаться между Slitaz и Windows, чтобы посидеть в Интернете. Но я все равно был счастлив: наконец-то я пользуюсь Linux!
Slitaz я запускал исключительно в режиме LiveCD, первое время не пытаясь установить систему насовсем. Хотелось сначала попрактиковаться на чем-то легковесном, а для постоянного использования найти что-то посерьезнее. Постепенно я перепробовал множество разных LiveCD: Puppy Linux, MCNLive, Austrumi, CDLinux и т.д. В каждом было что-то уникальное: например, MCN «из коробки» поддерживал Compiz — спецэффекты для окон.
Одним из самых интересных был дистрибутив Slax — он мог работать с флешки в режиме чтения/записи. При этом для систем, которые не поддерживали загрузку с флеш-накопителей, была предусмотрена возможность начальной загрузки с CD, а затем управление передавалось системе на флешке, и дисковод можно было освободить для других нужд. В Slax я просидел довольно долго, почти полгода — научился устанавливать пакеты, работал с Blender, GIMP, офисным ПО. Единственное, что портило настроение: система изредка могла намертво зависнуть — видимо, сказывались мизерные 512 Мб памяти при отсутствии своппинга.
И все же полноценным линуксоидом я себя считать не мог, пока не установил систему на жесткий диск. Случилось это летом 2009 года — тогда я как раз добрался до дистрибутива Mint. Интернет у меня тогда был временно отключен, и тут, как назло, слетела Windows Vista на одном из ноутбуков, к которому не прилагалась ОС на диске. Другого компьютера под рукой не было, но необходимо было срочно выполнить несложную офисную работу — OpenOffice Write было бы достаточно. Не оставалось ничего иного, как установить Mint — и в тот знаменательный день мои эксперименты с дистрибутивами, столь характерные для всех начинающих, благополучно завершились.
Система (если быть точным, Mint 6, основанный на Ubuntu 8.10) прекрасно встала на мое железо, без особого шаманизма заработало практически все периферийное оборудование, за исключением графического планшета — но его я впоследствии тоже сумел запустить. Это были времена расцвета GNOME 2: классический десктоп и привычный набор приложений делал миграцию с Windows легкой и безболезненной — «из коробки» шли традиционные GIMP, OpenOffice.org, Firefox, Thunderbird, Pidgin и т.д.
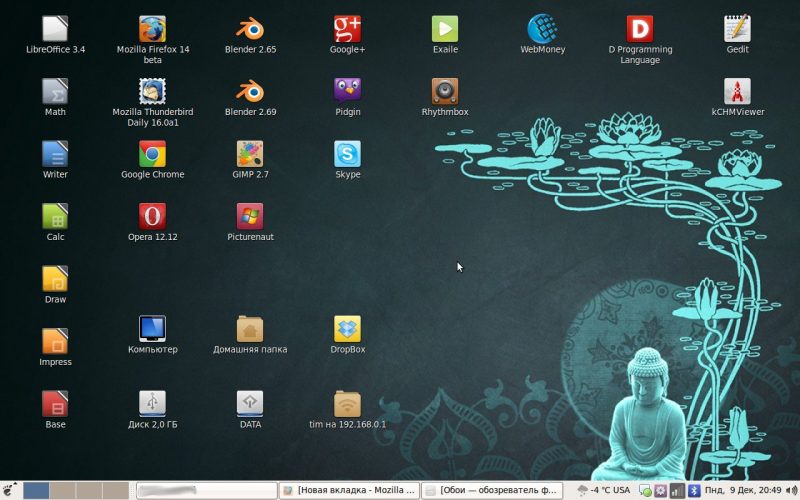 Производительность системы, по сравнению с Vista, поражала воображение: до этого я и не подозревал, что бюджетные ноутбуки способны включаться за десять секунд, а выключаться — за три!
Производительность системы, по сравнению с Vista, поражала воображение: до этого я и не подозревал, что бюджетные ноутбуки способны включаться за десять секунд, а выключаться — за три!
Mint 6 выжимал максимум из моей видеокарты: была поддержка OpenGL 1.4, но при этом — внушительный набор доступных расширений, в том числе GL_ARB_shading_language и GL_ARB_vertex_buffer_object. Для полного счастья не хватало разве что поддержки FBO. Конечно, без полной поддержки OpenGL 2.0 было невозможно играть в современные игры, но для работы в Blender и монтажа видео этого хватало с лихвой. Linux надолго продлил жизнь этого ноутбука.
Продолжение спустя 8 лет: Я возвращаюсь на Linux!